Hongyi Li's Machine learning course notes

Li's Machine-Learning

Model bias & Optimazition issue

训练过程中，先对 training data 的 loss 进行判定，如果大，则考虑两种情况

• 模型不够弹性（Model bias）
• 优化器做得不够好（Optimization）

搜索范围不够广还是优化器不能达到全局最优（SVM）？

如果发生下述情况，则说明优化器做得不够好 \[ \begin{array}{|c|c|c|c|c|c|} \hline & \text { 1 layer } & \text { 2 layer } & \text { 3 layer } & \text { 4 layer } & \text { 5 layer } \\ \hline 2017-2020 & 0.28 \mathrm{k} & 0.18 \mathrm{k} & 0.14 \mathrm{k} & 0.10 \mathrm{k} & 0.34 \mathrm{k} \\ \hline \end{array} \]

优化过程中 Loss 趋于不变，\(\nabla f\to 0\)，可能在 Local minima 或者 saddle point，区别方法：Hesse matrix 分别正定、既不正定也不负定 \[ L(\theta) \approx L\left(\theta^{\prime}\right)+\frac{1}{2}\left(\theta-\theta^{\prime}\right)^T H\left(\theta-\theta^{\prime}\right) \]

在鞍点处往 \(\lambda <0\) 对应的特征向量方向 \(\vec{u}\) 优化，\(H\vec{u}=\lambda \vec{u}\Longrightarrow L(\theta^{\prime})<L(\theta)\)，但实际中涉及二阶导和求解矩阵特征值运算，几乎不用。

维度高代表参数空间有更多的路可以走，实验给出，Hesse matrix 中特征值大于 \(0\) 的比例大多数集中在 \(0.5\) 附近，即多数情况下是卡在 saddle point。

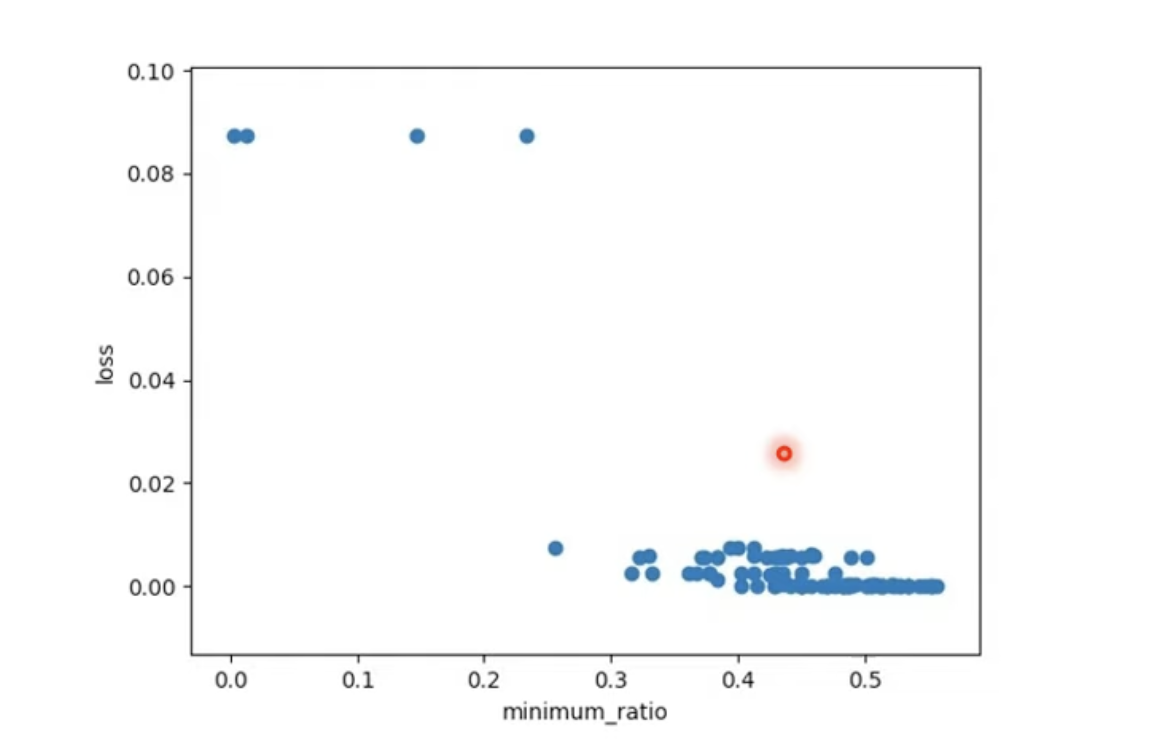
Critical point

Batch

不用所有的训练资料计算梯度，随机混合分组，每组 Batch 更新同一组参数，能够节约时间，虽然噪声影响大，但轮数多。（Batch 大不一定计算梯度时间长，现代硬件有平行运算能力）

大的 Batch-size 往往得到比较差的模型，在 Training data 和 Test data 上正确率都比较低，这是 Optimize 问题，因为不同的 Batch 形成的噪声能更好地跨过 saddle point。小的 Batch-size 在 Test data 上也表现好（一种解释是 Small batch 更容易进入“平原”）

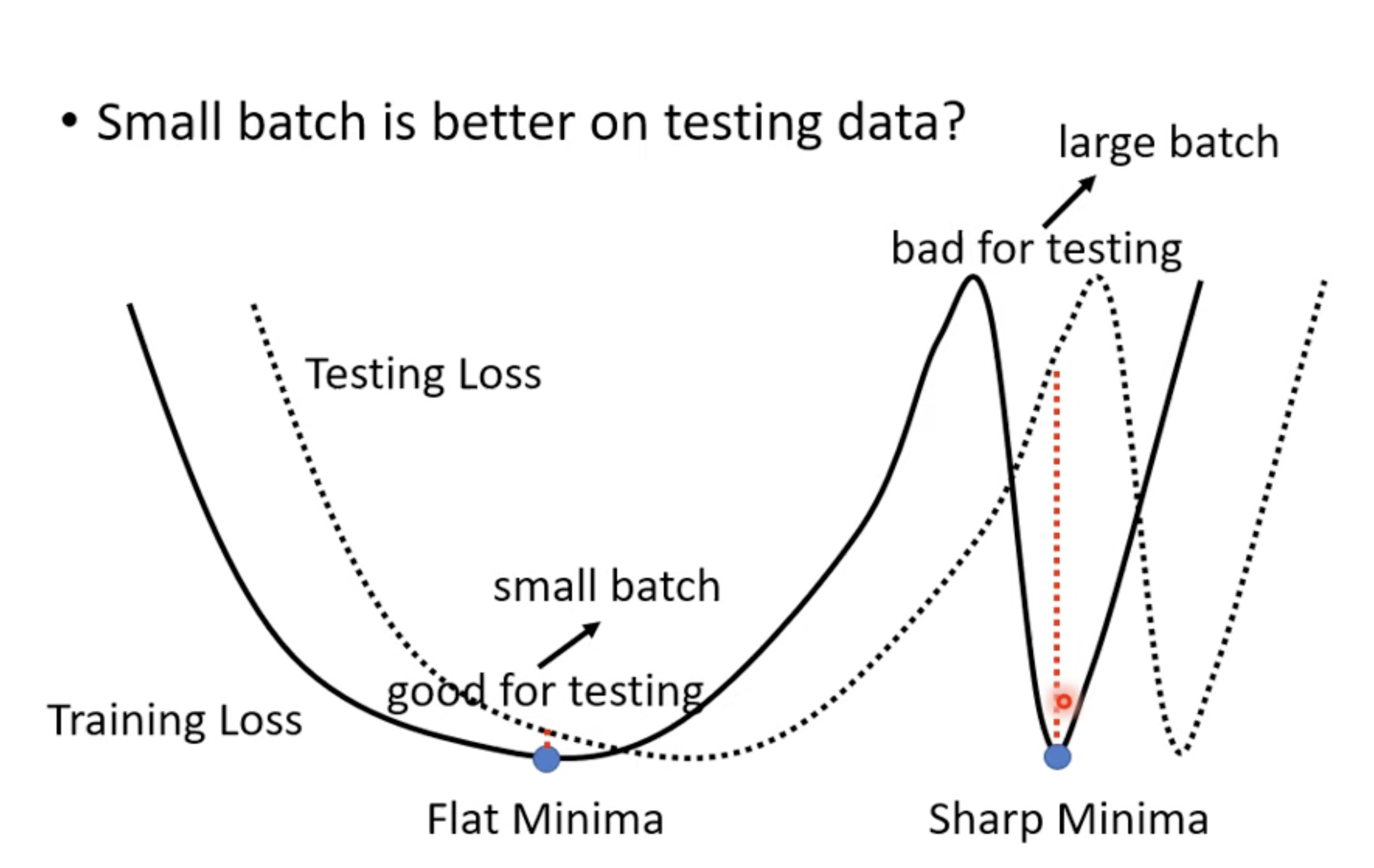
Momentum

在原始梯度下降（Vanilla）中加入惯性，引入 \(m^{i}\) 为每次改变中的质量，\(g^i\) 为每次计算的梯度 \[ \begin{aligned} m^2&=\lambda m^1-\eta g^1\\ \theta^2&=\theta^1+m^2 \end{aligned} \] 容易跨过鞍点

Learning_rate

Adam means Adaptive momentum.

Root Mean Square(Adagrad)

在一个等高线椭圆狭长的优化问题上优化

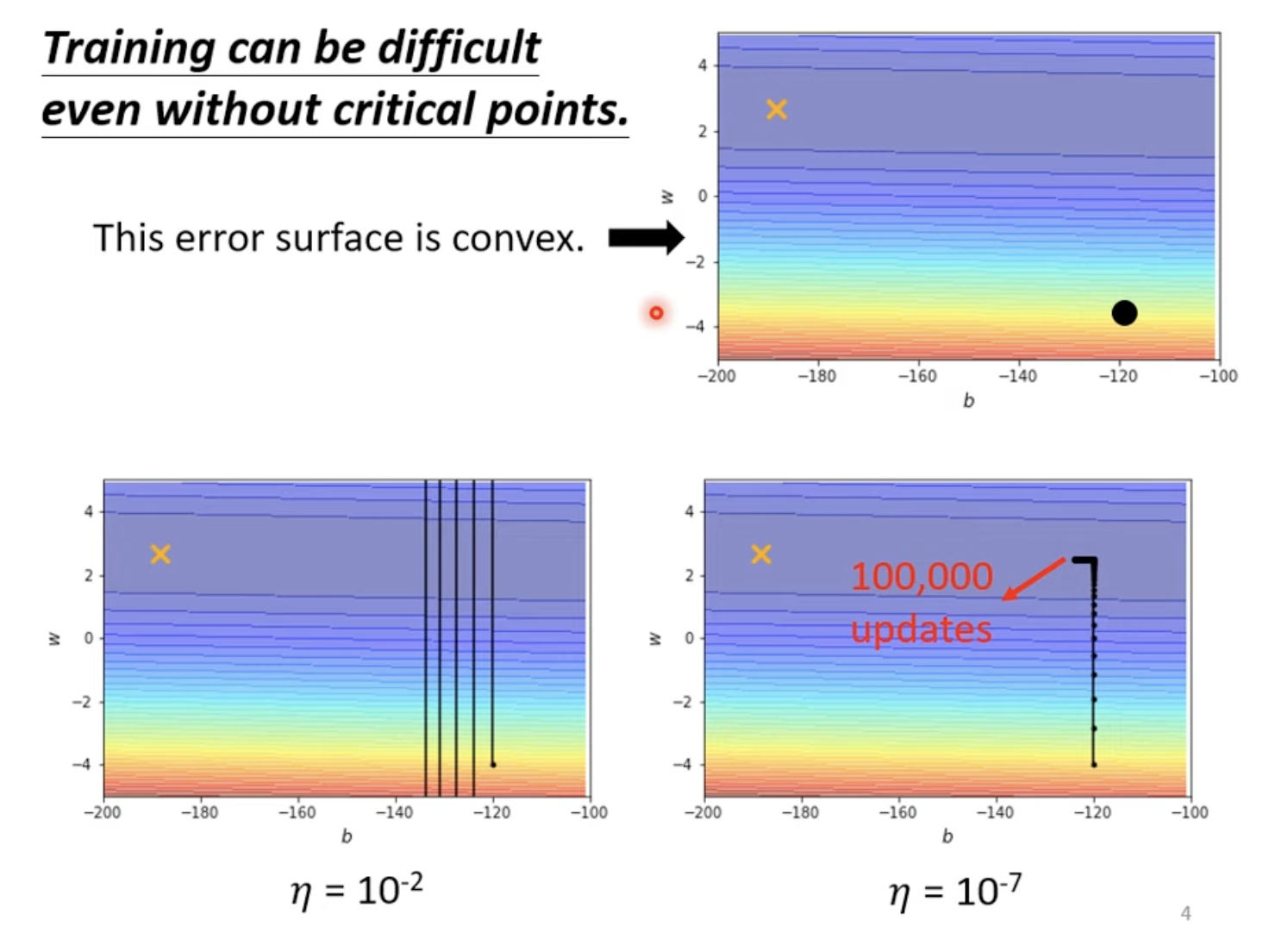
更新参数 \[ \theta_i^{t+1} \leftarrow \theta_i^{t}-\frac{\eta}{\sigma_i^t}g_i^{t} \] 对每个参数 \(i\)，使用前面梯度的方均根给参数 \(\sigma_i^t\)，如下 \[ \theta_i^{t+1} \leftarrow \theta_i^{t}-\frac{\eta}{\sigma_i^t} g_i^{t} \quad \sigma_i^t=\sqrt{\frac{1}{t+1} \sum_{i=0}^t\left(g_{\dot{i}}^{t}\right)^2} \] 即如果当前更新速度一直很慢的话可调大学习率，否则降低学习率

RMSProp

Google 使用的优化器

上述要求梯度基本一样，加入超参数 \(\alpha\) 表征前者调整的比例 \[ \theta_i^{t+1} \leftarrow \theta_i^{t}-\frac{\eta}{\sigma_i^t} g_i^{t} \quad \sigma_i^t=\sqrt{\alpha\left(\sigma_i^{t-1}\right)^2+(1-\alpha)\left(g_i^{t}\right)^2} \] Adam：RMSProp + Momentum

Learning Rate Scheduling

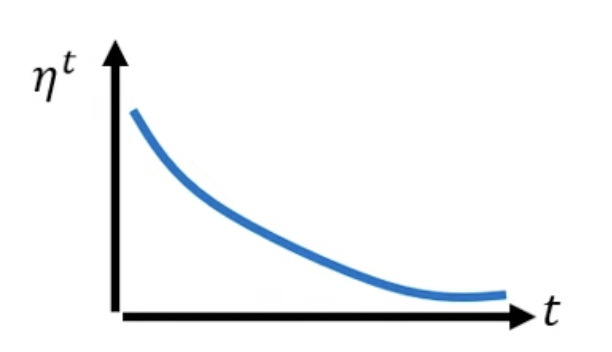
随着训练进行，将学习率本身不断减小

Warm-up 黑科技，在训练初期逐渐增加 Learning_rate，代表初期探索

Overfitting

上述过程均检测正常，即 training data 中 loss 较小，但 testing data 中 loss 较大，一个极端的例子是

Training data: \(\left\{\left(x^1, \hat{y}^1\right),\left(x^2, \hat{y}^2\right), \ldots,\left(x^N, \hat{y}^N\right)\right\}\) \[ f(x)=\left\{\begin{array}{cl} \hat{y}^i & \exists x^i=x \\ \text { random } & \text { otherwise } \end{array} \quad\right. \] model 越大，overfitting 的概率越大（另一种为 mismatch，就算有更多的资料，训练集和测试集的分布不一样）

解决办法：

• Data augmentation，将图片水平翻转或者放大让训练集变大

• Constrain，让模型限制在某些函数上

• 共用参数，限制参数 \[ \text{CNN}\in \text{Fully-Connected model} \]

• N-fold Cross Validation，提高 private-data 准确率

L2 正则化和 weight decay 是一样的，L2 正则就是权重衰减。