NLP introductory discussion notes

并行计算

并行技术综述

🚀—— 模型加速

• 数据并行：切分数据，调用 AllReduce 计算梯度均值
• 模型并行：将大模型 Tensor 切分计算，矩阵线性连接特性
• 流水并行：将任务分段，每个阶段在不同的设备上，前后阶段流水

🍴—— 减少存储

• 重计算：
  • 重新计算激活值
  • 转移到 CPU 上优化显存大小
• ZeRO 优化：分割模型和优化器，利用数据并行和模型并行的方式，减少单个设备上的内存占用。
• 1F1B：解决缓存 activation 的份数问题，使得 activation 的缓存数量只跟 stage 数相关。

模型加速

BSP / SSP

反向传播所需要的时间大约是前向传播的两倍（原因：反向传播需要访问当前输出值和梯度值，访问内存时间长，偏导数计算消耗大）

• BSP：每个 batch 的前向计算需要使用最新模型
• SSP：异步模型更新，后者收敛性没有被严格论证，不采用

以下为未改进 BSP 版本的运行方式，相比单机的改进仅仅是在最后 update 参数时可以并行更新

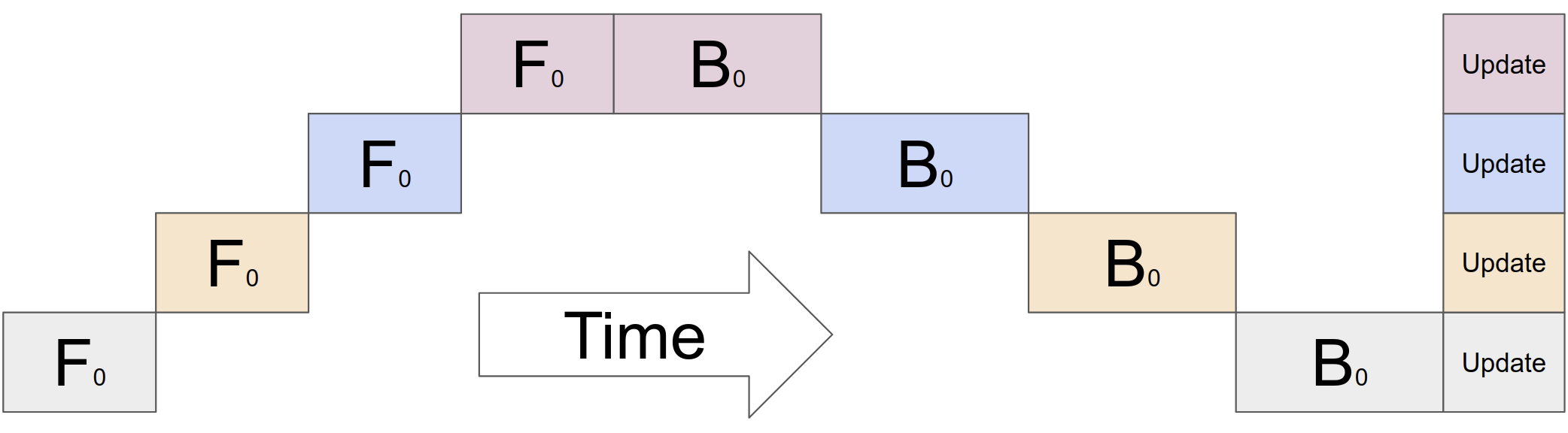
BSP 可以通过梯度累加和检查点加以改进，

梯度累加

数据并行是空间上的，数据拆分为多个 tensor，micro-batch 则是时间上的

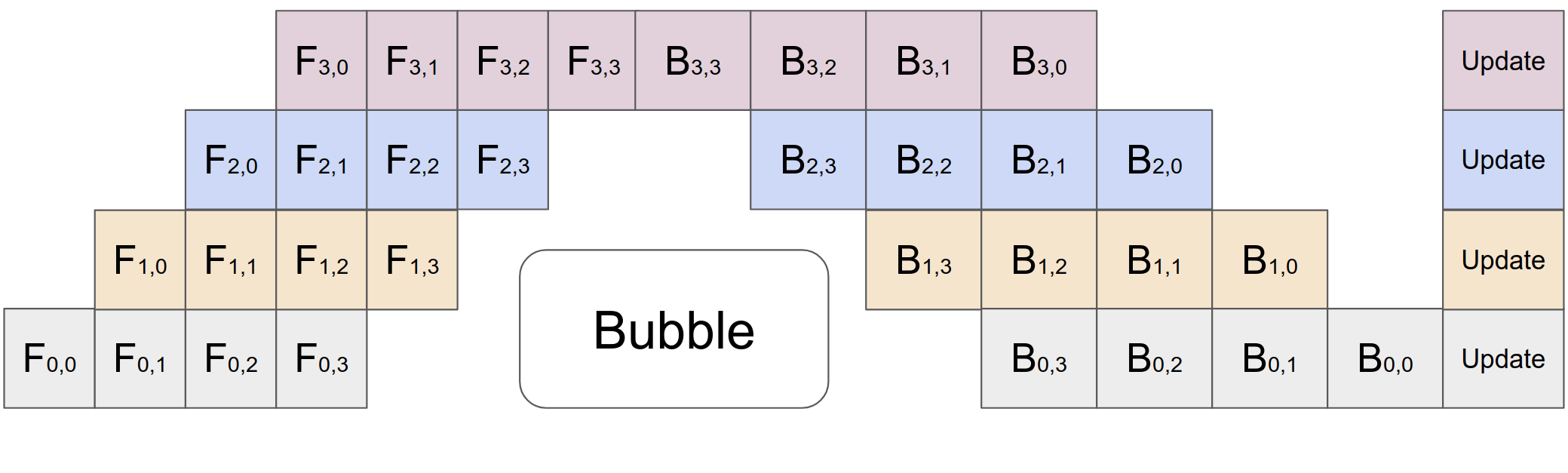
把前向传播和后向传播中的数据切分在时间序列上计算，记 stage 的数量为 \(p\)，切分数量为 \(s\)，可以推导气泡率 \(\eta\) 为 \[ \begin{equation} \eta=\frac{p}{p+s-1}+\epsilon(\epsilon>0) \end{equation} \] 可以理解为卡就在每两个 stage 之间的地方“等着"，micro-batch 鱼贯而入之后又鱼贯而出，每张卡把经过的每份子数据的前向激活值都存下来，子数据回传的时候把相应的前后值用作梯度计算并保存，当一张卡中所有的梯度计算完成之后更新参数。

利用率增加，但每张卡都要保存所有 micro-batch 的激活值，显存占用太大。

减少内存

后向重计算

又名“亚线性内存优化”

• Checkpoint：前向计算时只保留标记的 Tensor，其余通过反向传播时临时重新计算一遍前向。通过额外的计算开销减少显存。
• CPU offload：把暂时用不到的 activation 临时缓存到 CPU 上。通过额外的传输开销换显存。

1F1B

由公式 (1) 为减少气泡率，通常 \(p\sim 2s\)，但此时缓存数量较大，一种策略是在所有数据的前向传播未完成时开始反向传播，这样计算完之后的激活值可提早丢弃，其过程图如下，对每张卡实现前向后向交替使用

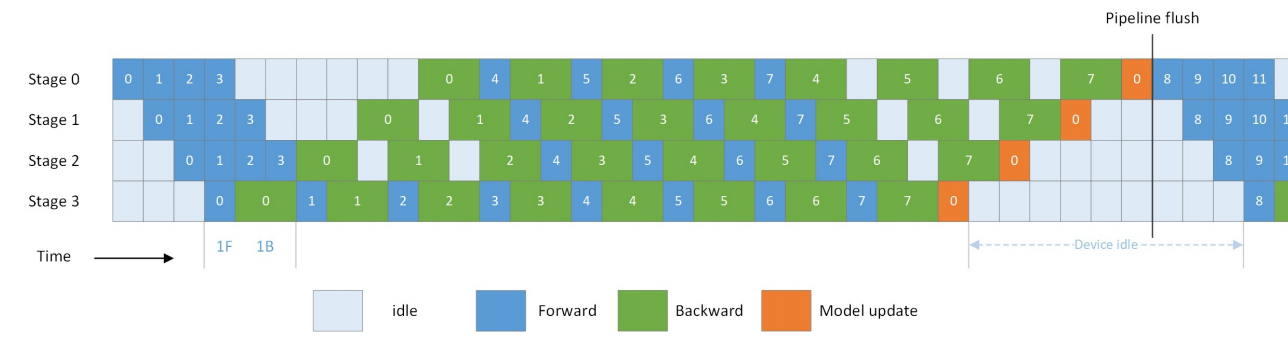
ZeRO

模型状态 (model states）：模型参数（fp16）、模型梯度（fp16）和 Adam 状态（fp32 的模型参数备份，fp32 的 momentum 和 fp32 的 variance ) 。假设模型参数量 \(\Phi\)，则共需要 \(2 \Phi+2 \Phi+(4 \Phi+4 \Phi+4 \Phi)=4 \Phi+12 \Phi=16 \Phi\) 字节存储, 可以看到，Adam 状态的参数量占比 \(75 \%\) 。

使用不同分割策略如下，Adam 的占用量最大，先从 Adam 下手，分别对应 ZERO_1, ZERO_2, ZERO_3

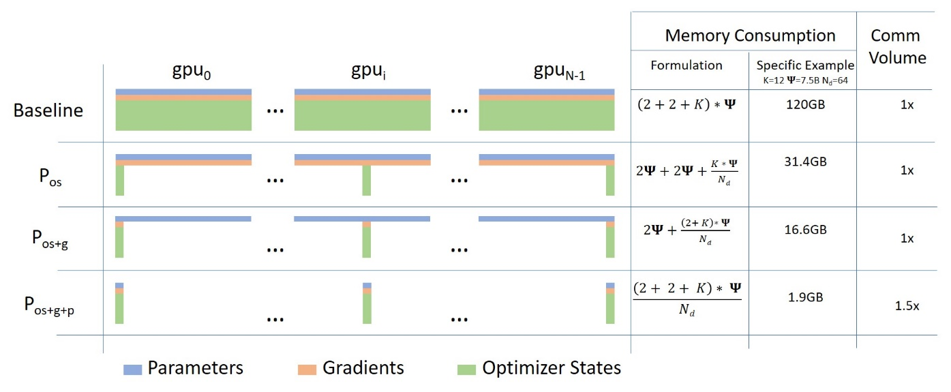
ZeRO-Offload

显存不够、内存来凑，不过需要消耗更多的通信时间

梯度累积次数

TP * PP 张卡去共用 MICRO_BATCH 样本，一共有 N 张卡，则每一次计算 \(\dfrac{\text{N}}{\text{TP}\cdot \text{PP}} \cdot\text{MICRO\_BATCH}\) 个样本，当梯度积累 \(\text{gradient}\) 次之后为 GLOBAL_BATCH 个样本时，进行一次梯度更新，从而 \[ \text{gradient}=\dfrac{\text{GLOBAL\_BATCH}}{\dfrac{\text{N}}{\text{TP}\cdot \text{PP}} \cdot\text{MICRO\_BATCH}}=\dfrac{\text{TP}\cdot\text{PP}}{\text{N}}\cdot\dfrac{\text{GLOBAL\_BATCH}}{\text{MICRO\_BATCH}} \] 要求 \[ \boxed{\text{TP}\cdot\text{PP}\mid\text{N}} \] 保证这 \(\text{N}\) 张卡以 \(\text{TP}\cdot\text{PP}\) 作切分，而本实验环境 \(\text{N}\) 是 \(8\) 的倍数，所以设置 \(\text{TP}\) 和 \(\text{PP}\) 等于 \(8\) 是理论可行的，但如果对于小模型仍旧让两者乘积等于 \(8\)，反而没能利用好显存